包括物理学、微积分是数学中的一门重要学科，它广泛应用于各个领域、工程学和经济学等。介绍如何利用微积分方法来计算各种形状的面积，本文将探讨微积分在计算几何面积中的应用。

什么是微积分

微积分是研究函数变化率和曲线与面积关系的数学学科。通过研究函数的导数和定积分来解决各种问题，它由微分学和积分学组成。

微积分中的导数和函数的变化率

描述了函数在某一点的斜率，导数是函数变化率的度量。我们可以获得函数在不同点上的变化率，通过求解导数，并进一步应用于计算面积问题中。

直线和曲线的长度计算

可以计算直线和曲线的长度，利用微积分方法。并对每个小线段的长度进行求和来计算曲线的总长度，我们可以通过将曲线分割成无限多个小线段。

矩形和平行四边形的面积计算

可以直接通过长度和宽度的乘积来计算其面积，矩形和平行四边形是最简单的几何形状。微积分方法可以将这一思想推广到更复杂的几何形状中。

三角形的面积计算

并计算每个小三角形的面积之和、可以用微积分方法来计算三角形的面积、通过将三角形分割成无限多个小三角形。这是利用定积分来计算面积的一种常见方法。

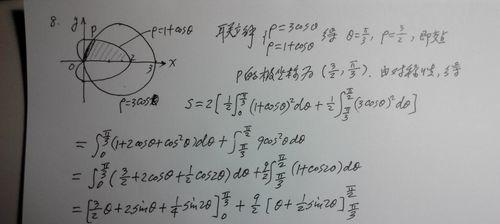
椭圆和圆的面积计算

它们的面积可以通过微积分方法来计算，椭圆和圆是常见的几何形状。我们可以得到准确的面积值、通过将椭圆或圆分割成无限多个小扇形、并计算每个小扇形的面积之和。

多边形的面积计算

可以利用微积分方法来计算其面积、对于规则或不规则的多边形。可以得到多边形的面积，并计算每个小三角形的面积之和，通过将多边形分割成无限多个小三角形。

曲线围成的面积计算

可以通过微积分方法来计算其面积、当曲线围成一个封闭的区域时。可以得到区域的面积，并计算每个小矩形或小三角形的面积之和，通过将区域分割成无限多个小矩形或小三角形。

平面图形旋转围成的体积计算

可以利用微积分方法来计算其围成的体积，当平面图形绕某条轴旋转时。可以得到旋转体的体积、通过将旋转后的曲线分割成无限多个小圆环、并计算每个小圆环的体积之和。

函数图形围成的面积计算

可以通过微积分方法来计算其面积、当函数图形和坐标轴围成一个封闭的区域时。可以得到区域的面积、并计算每个小矩形或小三角形的面积之和，通过将区域分割成无限多个小矩形或小三角形。

利用微积分解决实际问题中的面积计算

还可以应用于解决实际问题中的面积计算、微积分方法不仅可以用于几何图形的面积计算。可以计算出某个时间段内的总销售额等问题，通过对函数曲线下的面积进行积分。

微积分在计算面积中的局限性

通常假设曲线或区域具有平滑的特性、微积分在计算面积时。微积分方法可能无法直接适用、对于非光滑的曲线或不规则的区域。

数值方法在面积计算中的应用

可以使用数值方法来近似计算面积，当微积分方法无法直接适用时。并计算每个小区域的面积之和，可以得到一个近似值，通过将曲线或区域分割成多个小区域。

计算面积的应用领域

工程学，地理学和经济学等领域都有广泛应用，面积是几何学中一个重要的概念，在物理学。微积分方法为这些领域中的面积计算提供了有力的工具。

多边形和复杂图形的面积计算、曲线，可以应用于直线，微积分是计算几何图形面积的重要方法，通过研究导数和定积分。在实际问题中，我们需要根据具体情况选择合适的方法来解决面积计算问题，然而。